神经元更新#

作者: jing-alice & joyeewang

在神经元更新中，微分方程求解具有重要的地位和功能。神经元模型通常用微分方程描述其电生理特性和动态行为。这些微分方程描述了神经元膜电位、离子通道状态以及突触输入等随时间的变化规律。通过求解这些微分方程，可以模拟神经元的活动过程，包括动作电位的产生、神经元膜电位的变化以及突触传递的过程。

微分方程求解器#

本章将介绍如何使用 neurai.math 来解决不同种类的微分方程。在脑仿真过程中，需要通过求解微分方程来更新神经元的膜电压。 NeurAI 支持常微分方程（Ordinary Differential Equations，ODEs）和随机微分方程（Stochastic Differential Equations，SDES）的求解。

如何在NeurAI中定义微分方程?#

假设定义一个常微分方程：

\[\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0\]

然后可以将其转换成一个python函数：

def derivative(y):
  dy_dt = f(t, y)
  return dy_dt

此处， t 指当前时刻， y 指当前动态发生变化的变量。用户可以根据自己的需要自定义 \(f(t,y)\) 。

如何在NeurAI中定义常微分方程的求解器#

只需将上面定义的 derivative 函数传递给 ode.ode.ode_solve ，并通过 neurai.math.ode.ode.ode_solve 实例化一个对象，用户便可轻松地求解常微分方程。

from neurai.math.ode import ode_solve
from neurai.const import SolverMethodODE

diffeq_solve = ode_solve(differential_eq=derivative, method=SolverMethodODE.RK4)

ode_solve 接收多个参数，其中有两个参数用户必须传递。

differential_eq: Callable，指用户定义的微分方程；
method: SolverMethodODE，指用户选择的用于求解微分方程的方法。

如何使用常微分方程的求解器？#

最后，可以使用上面定义的求解器来求解并得到正确的结果。

y_new = diffeq_solve(y)

使用示例1：LIF模型#

以脑仿真中应用最广泛的泄露整合发放(LIF)神经元模型为例，来展示如何在NeurAI中定义并使用常微分方程求解器。

from jax import numpy as jnp
from neurai.math.ode import ode_solve
from neurai.const.math import SolverMethodODE

# parameters
v_rest = -60.
R = 1.
i_ext = 20.
tau = 20.
v = 0.

def derivative(v, v_rest, R, i_ext, tau):
  return (-v + v_rest + R * i_ext) / tau

v_list = []
diffeq_solve = ode_solve(differential_eq=derivative, method=SolverMethodODE.EULER)

for i in range(1000):
  v = diffeq_solve(v, v_rest, R, i_ext, tau, dt=0.1)
  v_list.append(v)

import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(jnp.asarray(v_list))
plt.show()

运行这个模型，结果是：

如何使用数值求解器求解微分方程组?#

在某些脑仿真情况下，我们会遇到包含多个变量的初始值问题，这些变量相互影响，需要定义和求解常微分方程组。

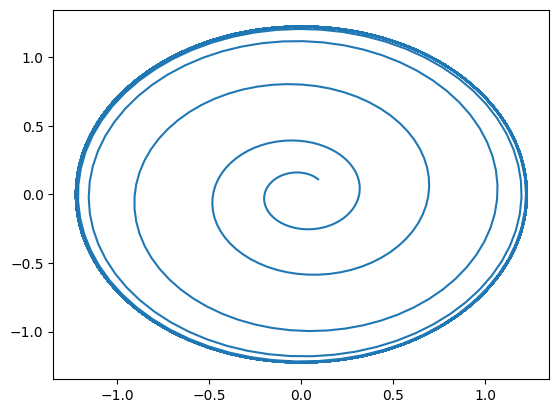
例如，霍奇金-赫胥黎（Hodgkin-Huxley，HH）模型中的V、m、h和n等相互依赖的变量需要同步更新。这里提供一个如何定义包含多个变量的常微分方程组的示例，以Hopf分岔为例，变量x和y相互影响，并动态更新。

import jax.numpy as jnp
from neurai.const.math import SolverMethodODE
from neurai.math.ode import ode_solve

mu = 1.0
w = 10.0

def dx_dt(x, y, mu, w):
  return (mu -x*x -y*y)*x - w*y

def dy_dt(y, x, mu, w):
  return (mu -x*x -y*y)*y + w*x

def all_dt(args: tuple, mu, w):
  x, y = args
  dx = dx_dt(x, y, mu, w)
  dy = dy_dt(y, x, mu, w)
  return(dx, dy)

diffeq_solve = ode_solve(differential_eq=all_dt, method=SolverMethodODE.EULER)

根据实际的微分方程定义Python函数 dx_dt 和 dy_dt。此外需要定义函数 all_dt 来构建微分方程组。需要注意的是，使用规范的函数的参数和返回值，所有变量都必须放在元组中，并返回元组。

x_test, y_test = [], []
x, y = jnp.ones(1) * 0.1, jnp.ones(1) * 0.1
for i in range(1,10000):
  x, y = diffeq_solve((x, y), mu, w, dt=0.01)
  x_test.append(x)
  y_test.append(y)

import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(jnp.asarray(x_test), jnp.asarray(y_test))
plt.show()

运行这个模型，结果是：

../_images/systemsofODE_Hopf_bifurcation.png

可提供的常微分方程求解器#

NeurAI 提供多种类型的ODE求解器，包括指数欧拉方法、显式龙格-库塔方法、自适应龙格-库塔方法、隐式欧拉等。用户可以通过在 neurai.math.ode.ode.ode_solve 中将方法指定为 neurai.const.math.SolverMethodODE 中的值来选择合适的方法。

1. 指数欧拉求解器#

首先，NeurAI为常微分方程提供指数欧拉求解器，其计算简单，可用于大多数场景。

Methods	SolverMethodODE
Exponential Euler method	EXP_EULER

示例代码如下：

from neurai.math.ode import ode_solve
from neurai.const.math import SolverMethodODE

def derivative(v):
  # parameters
  v_rest = -60.
  R = 1.
  i_ext = 20.
  tau = 20.
  return (-v + v_rest + R * i_ext) / tau

def decay_eq(v):
  tau = 20.
  return -1.0 / tau

diffeq_solve = ode_solve(differential_eq=derivative, method=SolverMethodODE.EXP_EULER)
v_new = diffeq_solve(-55., dt=0.1)

2. 显式龙格-库塔求解器#

NeurAI提供了不同阶数的显式龙格-库塔求解器，如RK2, RK3, RK4等，都展示在下表中：

Methods	SolverMethodSDE
Explict Runge-Kutta method	RK2
Explict Runge-Kutta method	RK3
Explict Runge-Kutta method	RK4
Explict Runge-Kutta method	MIDPOINT
Explict Runge-Kutta method	HEUN2
Explict Runge-Kutta method	HEUN3
Explict Runge-Kutta method	RALSTON2
Explict Runge-Kutta method	RALSTON3
Explict Runge-Kutta method	RALSTON4

3. 自适应龙格-库塔求解器#

不同于显式龙格-库塔求解器，NeurAI还设计了自适应龙格-库塔求解器，通过在单个步长求解的过程中估计截断误差来控制步长，如果 \({error} \gt {rtol}\) ，将 \({dt}\) 用 \({dt_{next}}\) 替换并重新计算直至在 \({dt}\) 内满足条件。

Methods	SolverMethodSDE
Adaptive Runge-Kutta method	RKF45

4. 隐式欧拉求解器#

隐式欧拉法（或后向欧拉法）也是求解常微分方程最基本的方法。后向欧拉方法计算近似值的方法如下：

\[y_{k+1} = y_{k} + hf(t_{k+1}, y_{k+1})\]

Methods	SolverMethodSDE
Implict Euler	IMPLICT_EULER

如何使用随机微分方程的数值求解器？#

不同于常微分方程，随机微分方程（SDE）是一个除了标准微分方程外，还带有内在噪声的系统，其中 \(g(X_{t},t)\) 是一个确定性函数，测量我们对某些标准噪声的敏感度。 \(W\) 表示维纳过程(标准布朗运动)。

\[dX_{t} = f(X_{t}, t)d_{t} + g(X_{t}, t)dW_{t}\]

所以可以像下面这样定义这两个python函数：

# dx(t) = -theta * x * dt + sigma * dw

def f(x):
# theta = 1
  return -x

def g(x, t):
  # sigma = 1
  return 1.0

可以使用Milsteain方法来解决这个问题：

from neurai.const.math import SolverMethodSDE
from neurai.math.sde import sde_solve

diffeq_solve = sde_solve(differential_eq=f, diffusions_eq=g, method=SolverMethodSDE.MISLTEAIN)

使用示例2：噪声洛伦兹系统#

使用著名的洛伦兹系统来演示在NeurAI中如何使用随机微分方程的数值求解器。

\[ \begin{align}\begin{aligned}\frac{d{x}}{d{t}} = \sigma(y-x) + px*dW_{x}\\\frac{d{y}}{d{t}} = \sigma x(p-z)-y + py*dW_{y}\\\frac{d{z}}{d{t}} = xy - \beta z + px*dW_{x}\end{aligned}\end{align} \]

from neurai.const.math import SolverMethodSDE
from neurai.math.sde import sde_solve
import jax.numpy as jnp

sigma = 10
beta = 8/3
rho = 28
p = 0.1

def lorenz_g(vars:tuple, t):
  x, y, z= vars
  dgx = p * x
  dgy = p * y
  dgz = p * z
  return (dgx, dgy, dgz)

def lorenz_f(vars:tuple, t):
  x, y, z= vars
  dx = sigma * (y - x)
  dy = x * (rho - z) - y
  dz = x * y - beta * z
  return (dx, dy, dz)


diffeq_solve = sde_solve(differential_eq=lorenz_f, diffusions_eq=lorenz_g,  method=SolverMethodSDE.MISLTEAIN)

sim_t = 50
dt = 0.001
t_test = jnp.arange(0, sim_t, 0.001)
x_test, y_test, z_test = [], [], []

x, y, z = 1, 1, 1
for i in range(50001):
  x,y,z = diffeq_solve((x,y,z), t = t_test[i], dt=dt)
  x_test.append(x)
  y_test.append(y)
  z_test.append(z)


import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.axes(projection='3d')
plt.plot(jnp.asarray(x_test), jnp.asarray(y_test), jnp.asarray(z_test))
ax.set_xlabel('x')
ax.set_xlabel('y')
ax.set_xlabel('z')
plt.show()

可提供的随机微分方程求解器#

NeurAI目前可以为随机微分方程提供两种类型的求解器。

Methods	SolverMethodSDE
Milsteain	MILSTEAIN
Heun	HEUN

神经元更新

Contents