伪梯度函数#

SNN中伪梯度函数的使用源于基于梯度的训练和反向传播的引入。传统的反向传播算法最初是为了训练人工神经网络（ANNs）而开发的，它使用具有连续导数的光滑激活函数（如Sigmoid或ReLU）。

然而，在SNNs 中，由于脉冲神经元的离散特性和阶跃式激活函数，出现不可导点。这使得直接应用传统的反向传播算法来训练SNNs变得具有挑战性。

为了解决这个问题，研究人员提出使用伪梯度函数。伪梯度函数近似并平滑离散非线性激活函数的导数，使在SNNs中基于梯度的训练和反向传播成为可能。通过使用伪梯度函数，可以在SNNs中完成梯度自动传播和优化，从而实现SNN基于梯度的学习和反向传播。

如，使用 Sigmoid 函数作为exodus中的伪梯度函数进行训练：

from neurai.grads import surrogate_grad
from neurai import nn
exodus_neuron = nn.Exodus(surrogate_grad_fn=surrogate_grad.Sigmoid(spiking=True))

参数：

spiking: 伪梯度函数是否应用于脉冲神经元或非脉冲（连续）神经元。如果为spiking= True ，在前向传播期间，即在发放脉冲阶段，将使用Heaviside函数，它根据输入是否超过一定的阈值输出0或1信号，在反向传播时使用所指定的伪梯度函数。如果为 False ，在前向传播期间将使用伪梯度函数对应的原始函数来计算。

Rectangular#

Rectangular 伪梯度函数收录自论文《Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks》(here)。

Rectangular 伪梯度函数定义如下：

\[h'(x) = \frac{1}{a} \cdot \text{sign}\left(\left|x\right| < \frac{a}{2}\right)\]

对应的原函数：

\[\begin{split}\mathrm{h}(x) = \begin{align*} \begin{cases} \frac{1}{\alpha} x + 0.5 & \text{if } |x| < \frac{\alpha}{2} \\ \text{c} \left( x + \frac{\alpha}{2} \right) & \text{if sign(x) = -1} \\ \text{c} \left( x - \frac{\alpha}{2} \right) + 1 & \text{otherwise} \end{cases} \end{align*}\end{split}\]

Polynomial#

Polynomial 伪梯度函数收录自论文《Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks》(here)。 Polynomial 伪梯度函数定义如下：

\[h'(x) = \left(\frac{\sqrt{a}}{2} - \frac{a}{4} \left|x\right|\right) \cdot \text{sign}\left(\frac{2}{\sqrt{a}} - \left|x\right|\right)\]

对应的原函数：

\[\begin{split}\begin{align*} \mathrm{mask0} &= (x > \frac{2}{\sqrt{\alpha}}) \\ \mathrm{mask1} &= (|\,x\,| \leq \frac{2}{\sqrt{\alpha}}) \\ \mathrm{h}(x) &= \text{mask0} + \text{mask1} \cdot \left(-\frac{\alpha}{8} \cdot x^2 \cdot \text{sign}(x) + \frac{\sqrt{\alpha}}{2} \cdot x + 0.5\right) \end{align*}\end{split}\]

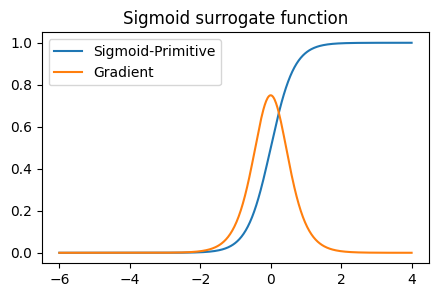
Sigmoid#

Sigmoid 伪梯度函数收录自论文《Spatio-Temporal Backpropagation for Training High- Performance Spiking Neural Networks》(here)。 Sigmoid 伪梯度函数定义如下：

\[h'(x) = a \cdot \frac{e^{-ax}}{(1 + e^{-ax})^2}\]

对应的原函数:

\[\mathrm{h}(x) = \frac{1}{1 + e^{-\alpha x}}\]

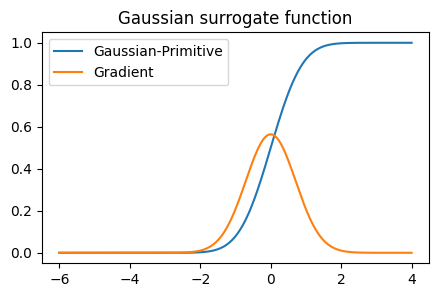
Gaussian#

高斯累计概率密度函数（CDF）[1] [2]作为代理梯度收录自论文《Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks》(here)。

\[h'(x) = \frac{1}{\sqrt{2\pi a}} \cdot e^{-\frac{(x)^2}{2a}}\]

对应的原函数:

\[\mathrm{h}(x) = \frac{{\text{erfc}(-\alpha x)}}{2}\]

其中erfc是 JAX 中的一个函数（jax.scipy.special.erfc），它用于计算补余误差函数 (Complementary Error Function)，通常表示为 erfc(x)。

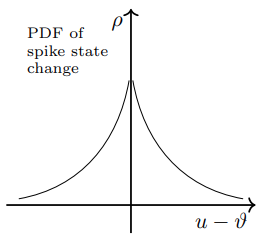
slayer_pdf#

在slayer中，伪梯度函数是神经元状态变化的概率密度函数(PDF)。slayer可以在脉冲神经元模型中引入随机性，并近似反向传播误差的导数。定义如下：

\[\rho(t) = \alpha e^{-\beta |u(t) - \theta|}\]

在这个公式中，\(\alpha\) 和 \(\beta\) 是控制PDF函数形状的参数。指数衰减确保PDF函数随着 \(u(t)\) 和 \(\theta\) 之间的差异的减少而增加。

以下是参考文章中提供的PDF函数示例。

SuperSpike#

该伪梯度出自于论文《SuperSpike: Supervised learning in multi-layer spiking neural networks》 (here)。

\[h(x) = \left( (1 + \beta |x - \theta|)^{-2} \right)\]

SuperSpike 方法利用一种特殊的伪梯度函数来近似脉冲神经元激活函数的导数。这种伪梯度函数在脉冲周围具有高斯形状，允许梯度随时间传播和更新。

SingleExponential#

该代理梯度收录自2013年Shrestha与Orchard合作的论文《SLAYER: Spike Layer Error Reassignment in Time》(here)。

在SNN网络的构建过程中，您需要选择适合您伪梯度函数，并将其作为参数提供给神经元模型的 surrogate_grad_fn 参数。在网络上的训练过程中，将根据所选的伪梯度函数进行梯度计算。

伪梯度函数

Contents