脉冲编码方式#

作者: Liuhui

脉冲神经元通过脉冲序列传递信息，为确保输入的有效性，通常需要使用脉冲编码方法将数值型数据转化为脉冲序列。这包括将连续数值转换为具有一定时间窗口的脉冲序列，其中时间窗口允许出现一个或多个脉冲。 脉冲编码方法通常用于将连续的实数值映射到脉冲神经元可以处理的离散脉冲序列。在这个过程中，输入信号的强度和时间信息被编码成神经元发放脉冲的频率和时刻。 常见的脉冲编码方式包括泊松编码、直接编码、时延编码。这些方法用于在脉冲神经网络中以脉冲的形式有效地表示和传输信息。

泊松编码#

使用泊松模型生成泊松脉冲序列的方法如下 ：

在长度为T的时间窗内，相邻脉冲时间间隔固定为1ms，对于每个间隔，从[0,1]区间内均匀分布生成随机数 \(rand_{i}(t)\)。将归一化的连续状态值 \(s_{p}(i)\) 视为产生脉冲的概率，如果 \(s_{p}(i)\) 大于或等于 \(rand_{i}(t)\) ，则发出脉冲；否则，不产生脉冲。

对于每个时间步 \(t\), 数学上可表示为 ：

\[\begin{split}poisson_{i}(t) = \begin{cases} 1 & \text{ if } s_{p}(i) >= rand_{i}(t) \\ 0 & \text{if } s_{p}(i) < rand_{i}(t) \end{cases}\end{split}\]
\[t = 1,2,3,.....,T\]

其中：

  • \(poisson_{i}(t)\) 为时间步长t的泊松脉冲序列。

  • \(s_{p}(i)\) 为归一化后的连续状态值。

  • \(rand_{i}(t)\) 为时间步长t产生的随机数。

该方法模拟了给定时间窗内泊松脉冲序列的生成过程，它由连续状态值和固定区间生成的随机数决定。

示例，对随机的MNIST数据集进行泊松编码：

from neurai.datasets.transforms import PoissonEncoder, LatencyEncoder, DirectEncoder
from neurai.datasets.mnist import MNIST
from neurai.datasets.dataloader import DataLoader
import matplotlib.pyplot as plt
import numpy as np

test_dataset = MNIST(root=DATASETS_DIR, train=False, download=False)
test_loader = DataLoader(dataset=test_dataset, batch_size=8, shuffle=True, drop_last=True)
T = 20

datasets = iter(test_loader)
data, label = next(datasets)

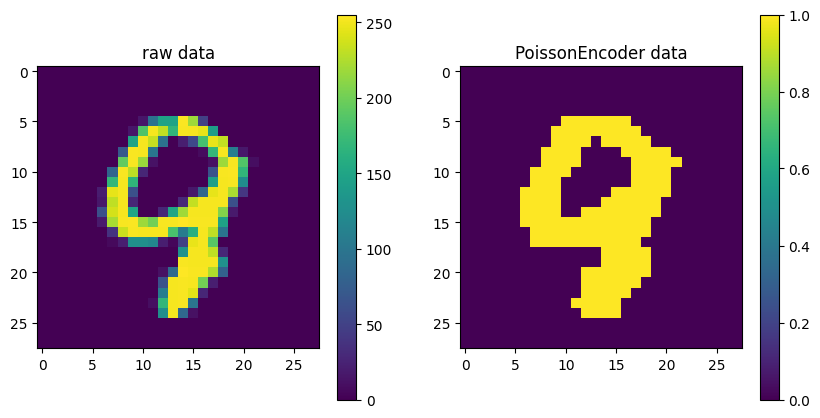
泊松编码后：

encoder = PoissonEncoder()
out_poisson = encoder(data)

# raw data
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(data[0, :, :, 0], cmap='viridis')
plt.title('raw data')
plt.colorbar()

# encoded data
plt.subplot(1, 2, 2)
plt.imshow(out_poisson[0, :, :, 0], cmap='viridis')
plt.title('PoissonEncoder data')
plt.colorbar()
plt.show()
poissonencoder

直接编码#

在直接编码中，数值直接映射到脉冲的时间和强度。数值较高时，会导致脉冲更频繁且强度更强；数值较低时，则会导致脉冲频率减少且强度减弱。这种编码方式实现了从输入数值到脉冲序列的直接映射。

数学上可表示为：

\[s_{p}(i) = \frac{abs(s_{b}(i))}{s_{max}(i)}\]
其中

  • \(s_{p}(i)\) 为时间步长i归一化后的状态值。

  • \(s_{b}(i)\) 为时间步长i归一化前的状态值。

  • \(s_{max}(i)\) 是时间步长i的状态的最大值。

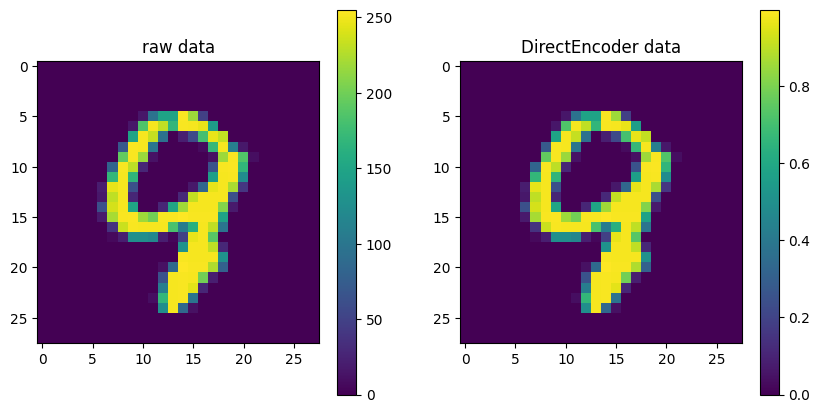
示例，对随机的MNIST数据集进行直接编码：

encoder = DirectEncoder()
out_direct = encoder(data)

# raw data
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(data[0, :, :, 0], cmap='viridis')
plt.title('raw data')
plt.colorbar()

# encoded data
plt.subplot(1, 2, 2)
plt.imshow(out_direct[0, :, :, 0], cmap='viridis')
plt.title('DirectEncoder data')
plt.colorbar()
plt.show()
directencoder

时延编码#

时延编码是对脉冲信号时间属性的一种抽象，信息被编码成首个脉冲释放后的延时。不同的时延代表不同的刺激强度，脉冲发放时刻越早，时延越短，刺激越强；脉冲发放时刻越晚，时延越长，刺激越弱。时延编码通过脉冲发放时间来表示数据大小的编码方式。利用下式来计算脉冲发放时刻。

可以用下式计算脉冲发放时间：

\[T_{first} = T-1-ln(a*s_{p}(i)+1)\]
其中：

  • \(T_{first}\) 表示首脉冲发放时间。

  • \(T\) 是总时间窗。

  • \(s_{p}(i)\) 为输入的状态值。

时延编码利用脉冲发放的定时来编码数据的大小，其中根据归一化状态值确定第一次脉冲发放的时间。

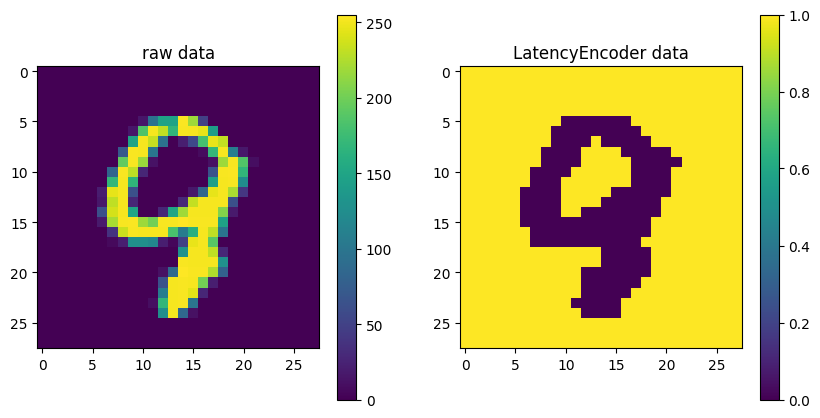
示例，输入图像，从MNIST中随机采样，经过Latency编码后：

encoder = LatencyEncoder(T)
out_latency = encoder(data)

# raw data
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(data[0, :, :, 0], cmap='viridis')
plt.title('raw data')
plt.colorbar()

# encoded data
plt.subplot(1, 2, 2)
combined_heatmap = np.sum(out_latency[0, :, :, 0, :], axis=-1)  # 在时间维度上求和

plt.imshow(combined_heatmap, cmap='viridis')
plt.title('LatencyEncoder data')
plt.colorbar()
plt.show()
latencyencoder